My research uses applied Mathematics in the following areas :
Nano structure evolution
Complex materials can evolve self-assembling nano-structures. For example, in Nafion, a membrane used in fuel cells, the dynamics of charged polymers in water self-assemble into a network of water pores.
The modelling effort focuses on a novel phase-field model for the self-assembly of pore networks and other morphologies. This model is very different from classical Cahn-Hilliard phase-field models, as it gives rise to a network formation process rather than a coarsening process. Our analysis at the sharp-interface limit gives riseto high-order Ricci-curvature flows, coupled to interfacial dynamics.
Simulation results for the self-assembling network model. The three different parameters lead to different network morphologies. All the simulations start with random initial data.
We validate our model by simulating a scattering curve for the pore network obtained numerically, see Figure below.
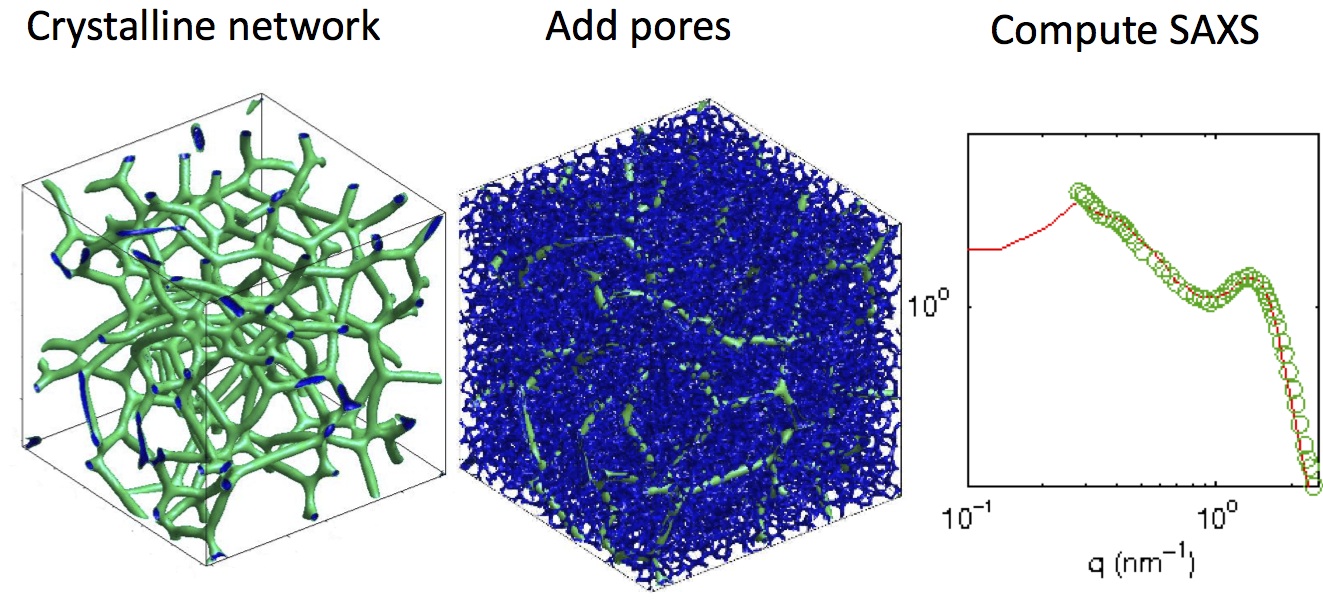
Crystalline (left) and water pore (center) networks. Right, a simulated scattering curve (red) is shown with experimental scattering data (green circles). From Rubatat et al., 2004.
A more detailed description of the research is available at this SIAM news article.
Auction theory
Auctions are important monetary tools, central to economic backbone. For example, in 2010 the US treasury auctioned securities in a total sum of 8.4 trillion dollars! Most of the literature on mathematical auction theory assumes that all players behave the same. Although this assumption is restrictive and often unrealistic, the symmetric case has the advantage that the optimal bidding strategy is given by a single differential equation and hence relatively easy to analyze.
I focus on a class of auctions in which no symmetry between the bidders is assumed, and, moreover, focus on large auctions which are most relevant to online auctions.
Nonlinear Schrödinger equation in the context of nonlinear Optics
The nonlinear Schrödinger equation (NLS) is one of the canonical nonlinear equations in physics, arising in various fields such as nonlinear Optics, plasma physics, Bose-Einstein condensates (BEC), and water waves. In nonlinear Optics it models the propagation of high power laser beams in media such as air, water or glass. It is well known that NLS solutions become singular at the point of collapse. One of the open questions in this field for more than 40 years is what is the behaviour of NLS solutions as they collapse. Since the 80s, the common perception is that all singular solutions of the NLS collapse with a single profile known as the Townes profile. This result served as a basis for essentially all the asymptotic theory of the NLS and of the perturbed NLS.
In my research I showed that this common perception is false, by showing that there are also NLS solutions that do not collapse with the Townes profile, but rather collapse with a ring profile. Moreover, we extended these results to a broader family of NLS equations (known as super-critical) [3]. Finding singular ring solutions for this family of equations involved constructing novel asymptotic structures.
My work involves continuous collaboration with the nonlinear Optics laboratory in Cornell University. Within this collaboration, our prediction of the new collapsing ring profile was confirmed experimentally. Moreover, we presented the first analytic method, known as the nonlinear Geometrical Optics method, for predicting the initial lamentation dynamics of high-power beams and pulses. This method allow control of the propagation dynamics of high-power lasers through the atmosphere. In addition, this method predicts a new type of temporal pulse-splitting, which was also confirmed experimentally within this collaboration.